Towards Live Programming Environments
for Statically Verified JavaScript
esverify.org/thesis
Christopher Schuster
University of California, Santa Cruz
cschuste@ucsc.edu
Motivation
Technology should not aim to replace humans, rather amplify human capabilities.
– Douglas Engelbart, 1958
Introduction
- A computer is a universal machine that can process any kind of information and perform any kind of computation
-
Computation and steps are specified with
a programming language
- very precise and technical
- unlike natural languages
- Programming is often tedious, frustrating and error-prone!
Program edits and feedback loop

Programming is an iterative cycle of code edits and feedback until the program behavior matches the intended behavior
Live programming environments improve this feedback cycle by enabling programmers to edit the code of running programs and obtain immediate feedback
Tests, Types and Program Verification
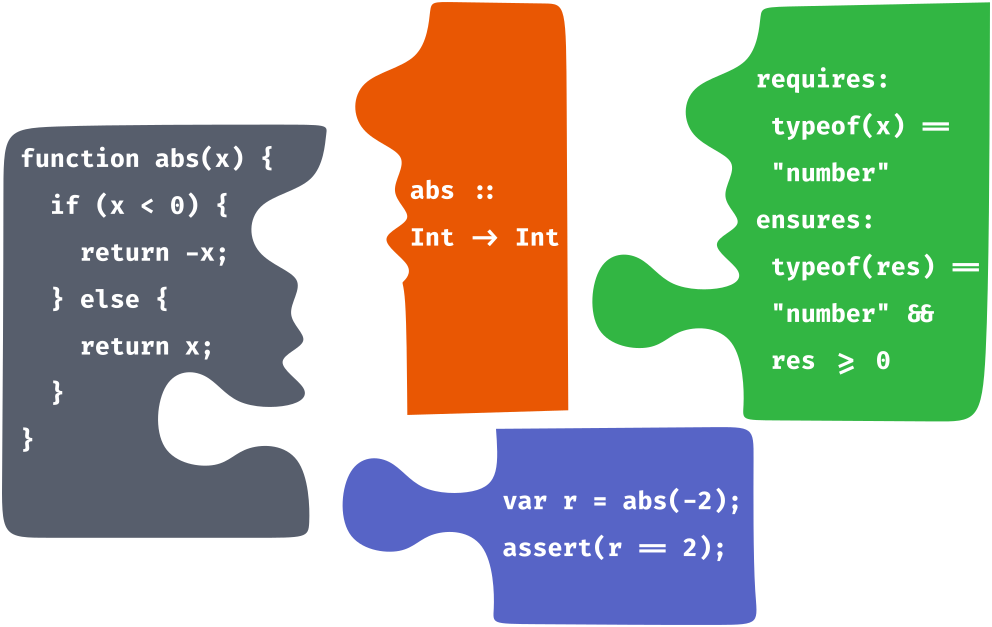
Check whether multiple specifications are consistent with each other and provide feedback about discrepancies
Outline
-
Live programming
- Live feedback for graphical applications based on a certain programming style
- Live programming by example/direct manipulation
-
Program Verification
- Static verification of dynamically-typed JavaScript, including higher-order functions
- Integrated Development and Verification Environments
Live Coding
An art or music performance in front of an audience (see e.g. Sam Aaron and Ben Smith)
Dynamic Software Updating
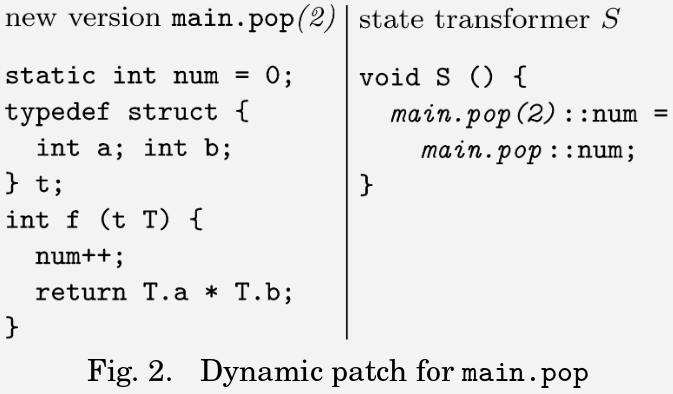
Patching running systems with explicit state migrations (see e.g. Michael Hicks and Scott Nettles)
Self-contained Development Environments
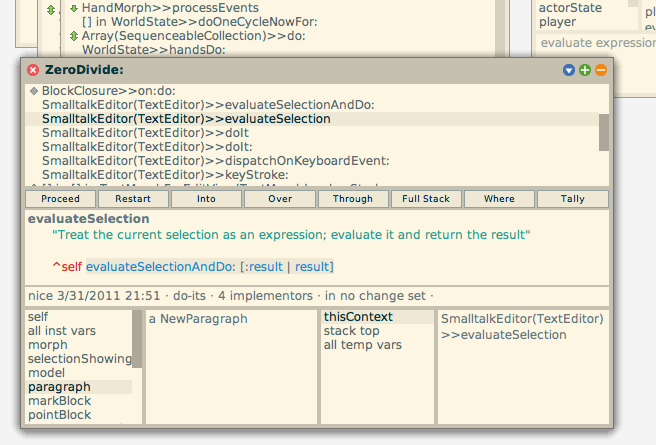
Environments with integrated development tools and runtime code updates (see e.g. Squeak Smalltalk)
Live Programming
Runtime code updates during the development process with explicit emphasis on immediate feedback (see e.g. Elm Debugger)
Live Programming
If there is any delay in the feedback loop between thinking of something and seeing it, then there is this whole world of ideas which will never be.
– Bret Victor
Code Updates and Execution State
Live Programming for GUI Applications
-
Single-threaded event loop (e.g. JavaScript)
- No code updates during events
- Pure Rendering Function to safely refresh output after each code update
- Closures do not persist between events
- See also Burckhardt et.al. 2013
"Traditional" UI Programming
1
2
3
4
5
6
7
8
9<span id="val">Count: 0</span>
<button id="incButton">+</button>
<script>
var count = 0;
$("#incButton").on("click", function () {
count++;
$("#val").html("Count: " + count);
});
</script>Problem: No live feedback for changes due to the structure of the code
Model-View-Update Pattern (MVU)
let count = 0;
function view() {
return (
<div>
Count: {count}
<button onclick={inc}>
Inc!
</button>
</div>);
}
function inc() {
count++;
}- Model holds entire application state
- View generates visible output based on Model
- Update processes events and changes the Model
Event Processing in MVU Applications
Live Edits to View Code
Live Edits to Update Code
Live Programming: Demo
Navigating Execution and Version History
Execution and Version History: Demo
Execution and Version History: Demo
Live Programming by Example
Demo
Dynamic String-Origin Tracking
String literals in the source code are wrapped in transparent proxies that track string origin information
let x = "ab"; x: [ ("ab", 9) ]
let y = x + "c"; y: [ ("ab", 9), ("c", 16) ]
let z = y[1]; z: [ ("b", 10) ]More complex programming-by-example introduces ambiguities
- Need heuristics/ranking or user interactions!
Summary
- live programming of the UI code,
- back-in-time debugging, runtime version control and
- live programming by example.
Outline
-
Live programming
- Live feedback for graphical applications based on a certain programming style
- Live programming by example/direct manipulation
-
Program Verification
- Static verification of dynamically-typed JavaScript, including higher-order functions
- Integrated Development and Verification Environments
Tests, Types and Program Verification


Check whether multiple specifications are consistent with each other and provide feedback about discrepancies
Automatic Unit Testing
- Testing only covers a certain set of example inputs
Type Checking
- Types are often not precise enough
- Dynamically-typed programming idioms not well supported
Program Verification
- Verification of pre-, postconditions and invariants often requires annotations and hints to the verifier
JavaScript Verification with esverify
- Pre- and postconditions, etc. written as standard boolean JavaScript expressions
- Annotations are used for static verification and removed before execution
-
Instead of type syntax,
the
typeofoperator can be used - Need to manually supply loop invariants and other verification hints
Another Verification Example
- Conjunction, disjunction and negation in logical annotations similar to union and intersection types
Verification Conditions
- Assertions are translated to logic and checked by SMT solving
Verification Conditions
function max(a, b) {
requires(typeof(a)=="number");
requires(typeof(b)=="number");
ensures(result => result >= a);
if (a > b) {
return a;
} else {
return b;
}
}
$ ~~~~~~\,\texttt{typeof}(a) = ``number'' $ $ \wedge~~~~\texttt{typeof}(b) = ``number" $
$ \wedge~~~~a > b~\Rightarrow~result\negmedspace=\negmedspace a$
$ \wedge~~~~\lnot (a > b)~\Rightarrow~result\negmedspace=\negmedspace b$
$ \Longrightarrow result \ge a $
Challenges for Verification:
Loops and Recursion
- Loops and recursion lead to unbound number of paths
- Inferring loop invariants and post-conditions undecidable
- Explicit postconditions and invariants required
Loops: Sum of Natural Numbers
function sumTo (n) {
requires(Number.isInteger(n));
requires(n >= 0);
ensures(res => res === (n + 1) * n / 2);
let i = 0;
let s = 0;
while (i < n) {
invariant(Number.isInteger(i));
invariant(Number.isInteger(s));
invariant(i <= n);
invariant(s === (i + 1) * i / 2);
i++;
s = s + i;
}
return s;
}
Function Definitions and Calls
function max(a, b) {
requires(typeof(a)=="number");
requires(typeof(b)=="number");
ensures(result => result >= a);
if (a > b) {
return a;
} else {
return b;
}
}
const x = max(23, 42);
assert(x >= 23);
$ \forall x. $
$ ~~~~ ( \forall a, b.~( $
$ ~~~~~~ \texttt{typeof}(a) = \texttt{"number"} ~\wedge~ $
$ ~~~~~~ \texttt{typeof}(b) = \texttt{"number"} ~\Rightarrow~ $
$ ~~~~~~ max(a, b) \ge a ) ) $
$ \wedge ~~~~ x = max(23, 42) $
$ \Longrightarrow x \ge 23$
Function Definitions and Calls: Details
- The pre- and postcondition of a function can be referred to with the uninterpreted construct $\texttt{pre} (f, x)$ and $\texttt{post} (f, x)$
-
A custom bounded trigger-based quantifier instantiation algorithm is used:
- Function calls act as triggers for a limited number of instantiations
- Avoids brittle instantiation heuristics, matching loops and SMT solver timeouts
Quantifier Instantiation (1/3)
function inc (x) {
requires(Number.isInteger(x));
ensures(y => Number.isInteger(y) && y > x);
return x + 1;
}
$ \forall x. \{ call(x) \} \Rightarrow $
$ \left( isInt(x) ~\Rightarrow~pre(\texttt{inc}, x) \right) ~\wedge~ \left( isInt(x) \wedge \,post(\texttt{inc}, x)~\Rightarrow~ \texttt{inc}(x) > x \right)) $
- $\{ call(x) \}$ is a trigger pattern
- $pre(\texttt{inc}, x)$ and $post(\texttt{inc}, x)$ uninterpreted function symbols
- $pre(\texttt{inc}, x)$ is satisfied by any integer value for $x$
- $post(\texttt{inc}, x)$ and precondition together imply $\texttt{inc}(x) > x$
Quantifier Instantiation (2/3)
function inc (x) {
requires(Number.isInteger(x));
ensures(y => Number.isInteger(y) && y > x);
return x + 1;
}
const y = inc(23);
assert(y > 23);
$ \forall y. $
$ ~~~~~~ \left( \forall x. \{ call(x) \} \Rightarrow \left( ...~\Rightarrow~pre(\texttt{inc}, x) \right) \wedge~ \left( ... \wedge \, post(\texttt{inc}, x) ~\Rightarrow~ ... \right) \right) $
$ \wedge ~~~~ call(23) $
$ \wedge ~~~~ post(\texttt{inc}, 23) $
$ \wedge ~~~~ y = \texttt{inc}(23) $
$ \Longrightarrow y > 23 $
Quantifier Instantiation (3/3)
function inc (x) {
requires(Number.isInteger(x));
ensures(y => Number.isInteger(y) && y > x);
return x + 1;
}
const y = inc(23);
assert(y > 23);
$ \forall y. $
$ ~~~~~~\, \left( isInt(23) ~\Rightarrow~pre(\texttt{inc}, 23) \right) $
$ \wedge~~~~ \left( isInt(23) ~\wedge~post(\texttt{inc},23)~\Rightarrow~ \texttt{inc}(23) > 23 \right) $
$ \wedge ~~~~ post(\texttt{inc}, 23) $
$ \wedge ~~~~ y = \texttt{inc}(23) $
$ \Longrightarrow y > 23$
Higher-order Functions: Twice
function inc (x) {
requires(Number.isInteger(x));
ensures(y => Number.isInteger(y) && y > x);
return x + 1;
}
function twice (f, n) {
requires(spec(f, (x) => Number.isInteger(x),
(x,y) => Number.isInteger(y) && y > x));
requires(Number.isInteger(n));
ensures(res => res >= n + 2);
return f(f(n));
}
const m = twice(inc, 3);
assert(m >= 5);
Challenges for Verification:
Recursive Data Types
- Nested recursive data structures (records, lists, trees)
- Proposed Solution: Simple immutable "classes" with invariants
- Check invariant when creating instances
- Instantiate invariant when accessing properties
Simple Immutable Classes: Adder
class Adder {
constructor (base) {
this.base = base;
}
invariant () {
return Number.isInteger(this.base);
}
addTo (n) {
requires(Number.isInteger(n));
return this.base + n;
}
}$ \forall x. \{ access(x) \} \Rightarrow \left( ~x ~~\texttt{instanceof} ~~ \texttt{Adder} ~\Rightarrow~ isInt(x.base) \right) $
Case Studies
- Reversing an ascending list yields a descending list
- A verified implementation of MergeSort
- A custom list class that can be parameterized by an invariant (somewhat analogous to generics)
- A theorem and proof written in JavaScript showing that any locally increasing integer-ranged function is globally increasing
About 50-80% of source code are verifier annotations
Formal Development with $\lambda^S$
- Pure functional core language with logical propositions as pre- and postconditions
- Verification rules similar to typing rules but also generate verification conditions
-
Verification is sound:
- Verified programs execute without getting stuck
-
Verification algorithm is decidable
- Decision procedure terminates for all inputs
- Complete mechanized proof in Lean
Refinement Typing with $\lambda^T$
$T \in \text{Types} ~::=~ \{~x: B~|~ R~\} ~|~ x:T \rightarrow T \hspace{2.5em} B ~::=~ \text{Bool}~|~ \text{Int}$
-
Refinement types translate to annotations
- Dependent function types translate to
spec
- Dependent function types translate to
-
Conjuecture that well-typed programs translate to verifiable programs
- Proof is work in progress
Summary
- Static program verification can be applied to dynamically-typed JavaScript programs including higher-order functions
- A custom quantifier instantiation ensures that the verification process remains predictable
- Verification is sound and (seemingly) at least as expressive as refinement type systems such as LiquidHaskell
Outline
-
Live programming
- Live feedback for graphical applications based on a certain programming style
- Live programming by example/direct manipulation
-
Program Verification
- Static verification of dynamically-typed JavaScript, including higher-order functions
- Integrated Development and Verification Environments
Verification Issues and Tool Support
-
Verification issues can be hard to understand and fix
due to expressive logic and complex verification procedure
- Simple error messages inadequate
- Explain verification issues with executable counterexamples (tests)
- An integrated Verification Inspector can show details about a verification issue and enables interactive exploration
Counterexamples and Test Generation
- SMT solver returns values for free variables
- Can automatically generate test based on original code and counterexample values
- Annotations become dynamically-checked assertions in the test
- For higher-order functions, this includes synthesis of function values and contract checking
Counterexamples as Editor Tooltips
Verification Inspector
Integrated Debugger
User Study
- Evaluated the development environment with verification integration with an online user study with 18 participants
-
User study involved:
- a tutorial,
- a series of programming and verification tasks, and
- a survey.
-
Archived user study:
esverify.org/userstudy-archived
User Study Results
| Response (%) | Verification Inspector | Counterexample Popups | Integrated Debugger |
|---|---|---|---|
| Helpful | 33 | 55 | 44 |
| UI Issues | 50 | 39 | 44 |
| Not useful | 6 | 6 | 6 |
| Impairs development | 11 | 0 | 6 |
Summary
- Verification errors can be difficult to understand
- Executable counterexamples and tool integration can assist programmers
- A novel Verification Inspector enables programmers to interactively add or remove assumptions and assertions
- Features are generally seen as helpful by user study participants
Conclusions
To improve our collective ability to solve the world’s problems, we must harness the immense promise and power of technology.
– Douglas Engelbart
Conclusions
-
To solve problems with technology,
programmers need to communicate the intended program behavior
- Independent of future advances in artificial intelligence
-
Programming is an iterative process
- Programming environments should aim to provide immediate live feedback for any change to the code
-
Static verification enables programmers to specify detailed invariants
and check the implementation
- Interactive tools and environment integration is crucial to make verification usable in practice
Related Work and Acknowledgements
- Live programming: Elm, TouchDevelop (especially the It's Alive paper), Jonathan Edwards (including Subtext), and Smalltalk environments such as Squeak and Lively Kernel, everyone at CDG/Y Combinator Research.
- Program Verification: Dafny, LiquidHaskell and Lean
- Finally, thanks to my advisor, Cormac Flanagan, the programming language group at UC Santa Cruz and my PhD committee.
Thank you for your attention!
Questions?
esverify.org/thesis
User Study Results (2/2)
| Response (%) | Verification Inspector | Counterexample Popups | Integrated Debugger |
|---|---|---|---|
| Used this feature in experiments | 39 | 50 | 28 |
| Unsuccessfully tried using it | 33 | 33 | 22 |
| Did not use it | 27 | 17 | 50 |