Towards Live Programming Environments for Statically Verified JavaScript
Christopher Schuster, December 2018
This page gives a brief summary of my PhD thesis with interactive demos and illustrations. The full thesis as PDF can be found here. On a high level, the thesis consists of three parts:
Introduction
Programming is often tedious, frustrating and error-prone because it involves specifying the intended behavior of a computer program in a very precise and technical programming language. Unlike communication in a natural language, programming is generally a process of trial-and-error.
Nobody actually creates perfect code the first time around, except me. But there's only one of me. – Linus Torvalds ↗
In addition to the programming language, the programming environment itself should be considered for new solutions that support this iterative process of code edits and feedback.
In order to improve this process with more immediate feedback, live programming environments enable programmers to edit the code of running programs and thereby observe the effects of the edit without having to re-compile and restart the program.
 Programming as an iterative cycle of code edits and feedback until the program behavior matches the intended behavior.
Programming as an iterative cycle of code edits and feedback until the program behavior matches the intended behavior.Furthermore, programming environments can check whether multiple specifications are consistent with each other and provide feedback about potential discrepancies. For example, the program code can be checked against automatic unit tests, types annotations or logical expressions such as invariants, pre- and postconditions and assertions (program verification).
 By describing the program behavior in multiple different ways, any mismatch can be detected automatically. More detailed and precise descriptions result in a higher redundancy and thereby a higher chance to find discrepancies (and potential bugs).
By describing the program behavior in multiple different ways, any mismatch can be detected automatically. More detailed and precise descriptions result in a higher redundancy and thereby a higher chance to find discrepancies (and potential bugs).As part of my thesis research, I made contributions to both live programming and program verification and thought about ways to integrate both in a programming environment.
Live Programming Environments for JavaScript
The term live programming is closely related (and sometimes confused with) concepts such as live coding, dynamic software updates and self-contained environments.
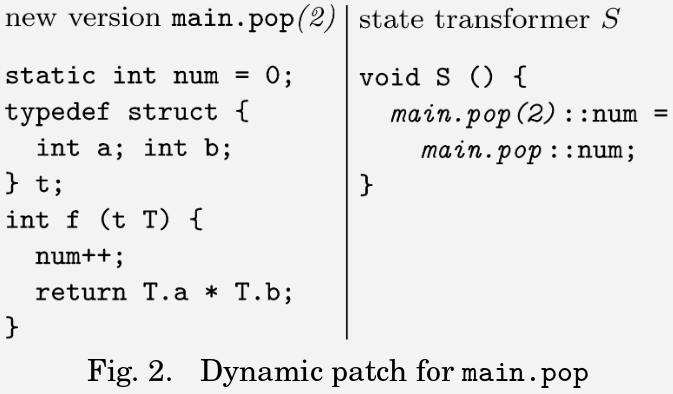
patching running systems with explicit state migrations
see e.g. Michael Hicks and Scott Nettles ↗
environments with integrated development tools and runtime code updates
see e.g. Squeak Smalltalk ↗
runtime code updates during the development process with explicit emphasis on immediate (or even continuous) feedback
see e.g. Elm Debugger ↗
If there is any delay in that feedback loop between thinking of something and seeing it and building on it, then there is this whole world of ideas which will never be.
– Bret Victor ↗
Live code updates of running programs can be tricky because the previous execution state may not be compatible with the new code.
- Problem 1 Where and how does the execution resume if the currently executed expression, statement or function is changed or removed?
- Problem 2 How can the visible output be updated to reflect the new version of the code?
- Problem 3 How are function values (closures) maintained if the surrounding code is modified?
- Problem 4 What happens if the format or shape of application is changed in an incompatible way?
Some of these problems can be resolved by restricting update points and imposes a certain programming model.
Proposed Solutions: Next
Unfortunately, there is no automatic unambiguous way to migrate existing application data if the data format changes. The programmer has to either supply an explicit state transformer/schema migration or restart the program.
Separating Rendering from Event Handling (MVU)
Certain programming styles make live programming extremely difficult. The following example uses jQuery to registers an event handler for the button and to update the display with the current click count.
1
2
3
4
5
6
7
8
9<span id="val">Count: 0</span>
<button id="incButton">+</button>
<script>
var count = 0;
$("#incButton").on("click", function () {
count++;
$("#val").html("Count: " + count);
});
</script>If the programmers wants to change "Count:" to "Clicks:", the programming environment should update both the visible output and the event handlers used for subsequent clicks. This essentially involves registering new event handlers (re-evaluating line 5) and updating the output (re-evaluating line 7) without changing the current application state (not re-evaluating line 6).
There are many different approaches and programming styles that advocate for a more declarative style that separate the rendering code from the event handling code. For an overview, see André Staltz.
Here, we adopt the Model-View-Update (MVU) pattern, which is similar to the Elm Architecture.
let count = 0;
function view() {
return (
<div>
<span>
Count: {count}
</span>
<button onclick={inc}>
Inc!
</button>
</div>
);
}
function inc() {
count++;
}encompasses the entire application state including the UI state
in this case a simple global variable
View
:: Model -> Output
returns the output/user interface based on the current model
should not mutate the model!
in this case, a JSX/React-style notation is used for inline HTML
Update
:: Model × Event -> Model
processes events, yielding a new model
in this case just mutates the global variable
Rendering the entire user interface each time may incur a performance overhead but this could be avoided or mitigated with techniques such as reactive programming and differential updates of virtual DOMs.
Live Code Updates and Time Travel
With the MVU pattern, the programming environment can re-render the output on demand. In particular, to provide feedback for live code updates.
The following demo shows an small live programming environment for MVU applications.
The editor on the left allows live code updates. In particular, changing "Count:" to "Clicks:" yields immediate feedback in the output. Changes to the model (i.e. the global variables) require a restart to take effect.
By re-rendering the output on demand, the programming environment can additionally provide live feedback for past states of the execution (back-in-time debugging) and for previous versions of the view code (runtime version control).
The programming environment can provide immediate feedback for input events and code updates but also for restoring previous version of the code or going back-in-time to previous models. This enables navigation of application states and code versions on two dimensions. Next
The following live programming environment is augmented with controls for going back to previous states and versions of the code.
This editor has a panel on the right that allows navigating to previous versions of the code and past application states.
Here is another example of an interactive game inspired by Flappy Bird.
In addition to live code updates and back-in-time debugging, an additional button can be used to start and stop the animation. Clicking in the output makes the bird fly up. Art by jsstrn ↗ and GDJ ↗.
The programming environment ensures re-rendering after events, it manages state snapshots for back-in-time debugging, it prevents mutation to the application state during rendering, and it checks the state for closures.
Live Programming by Example
The live programming environment described above enables the programmer to update the view code and get live feedback. Based on this concept, the environment can also support programming-by-example such that the programmer supplies an example output and the system automatically infers and updates the view code.
Depending on the concrete implementation, different kinds of direct manipulation and different inference algorithms could be supported.
In the following example, stopping the execution makes any text in the output editable. In particular, "Demmo" can be changed to "Demo" simply by pausing the execution, clicking on the text and then deleting the superfluous "m". These changes can also be made in the raw HTML representation of the output.
This prototype implementation only allows edits to string literals appearing in the source code. Internally, this is implemented by rewriting the source code such that string literals are wrapped in transparent proxies that track string origin information (even when strings are manipulated with operators).
let x = "ab";
let y = x + "c";
let z = y[1];x: [ ("ab", loc: 9) ]
y: [ ("ab", loc: 9), ("c", loc: 16) ]
z: [ ("b", loc: 10) ]Changing string literals in the program by manipulating text in the output avoids ambiguities that are common in program synthesis applications. More sophisticated approaches have to address these ambiguities with heuristics or manual user intervention. For example, the programming environment might present a ranked list of code candidates for the programmer to choose from.
To summarize: By restricting the programming model to follow an event-based MVU architecture, the programming environment can support runtime code updates with live feedback, back-in-time debugging, runtime version control and live programming by example.
JavaScript Program Verification
As mentioned in the introduction, programming environments can also provide feedback by automatically checking the implementation (the executable specification) against other specifications of expected behavior, such as tests and types. Both testing and type checking have become a successful and popular part of software development but they also have limitations.
Automatic unit testing only compares the expected behavior for certain example values, so no amount of testing can cover all possible inputs.
Typechecking also falls short for this particular example because it relies on a type language that is often too imprecise to express the expected behavior.
Furthermore, static typechecking also affects the code style. Some dynamically-typed programming idioms are not well supported and need to be avoided despite commonly used in JavaScript. In the example below, x can be a string, a string function or a generic type T. The code only calls x() if it is a function but TypeScript cannot accommodate this pattern.
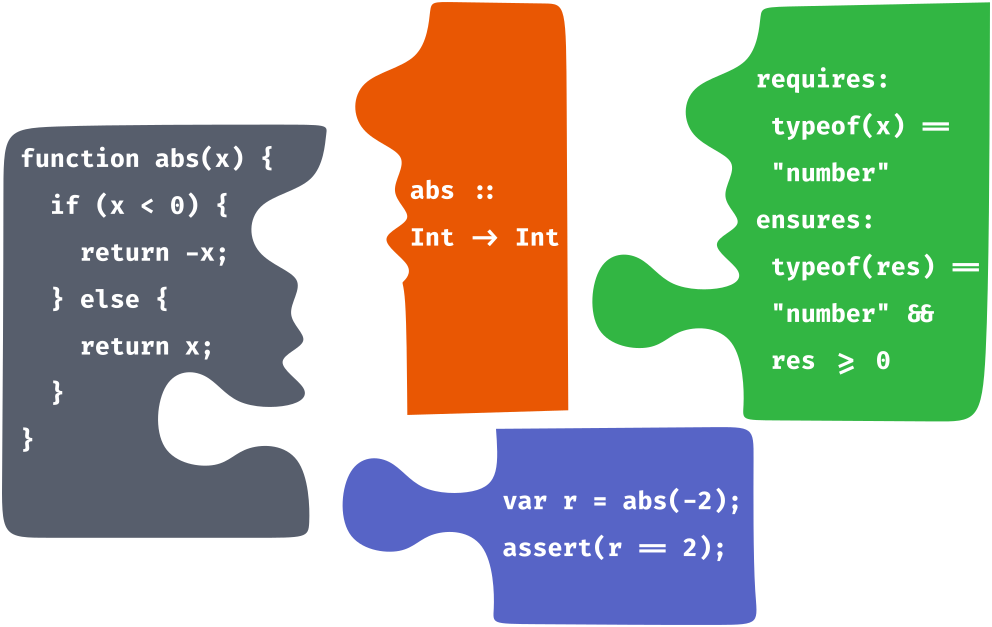
Example
- The calls to
requiresandensuresin lines 2-5 are only used for verification purposes and skipped during execution. - Instead of type annotations, the standard
typeofoperator is used to restrict the argumentsaandb. - Due to a bug in line 9, the
maxfunction does not return the maximum ifbis greater thana; violating the postcondition in line 5.
With conjunction, disjunction and negation, logical annotations can express detailed specifications, similar to union and intersection types and possibly going beyond.
Annotations and SMT solving
Internally, the program verifier translates the annotations as well as the implementation code into a logic. Each assertion, postcondition, etc. then corresponds to a verification condition that is passed to an SMT solver such as z3 or CVC4.
The following example shows a simple assertion that is translated to logic and statically verified.
The original JavaScript code is on the left, the middle pane shows the verification condition and the right pane displays the (partial) SMTLIB 2 input for the solver.
For the max function above, the SMT solver finds and returns counterexample that refutes the verification condition.
Mutable variables are represented by references to heap contents $H_n$. The special syntax old(x) can be used to refer to previous values.
Loops and recursion lead to an unbound number of code paths and pose a challenge for verification. Therefore, explicit loop invariants and postconditions are necessary. The following example sums up the first $n$ natural numbers and proves that the result is equal to $\frac{n^2 + n}{2}$.
Function Calls and Quantifier Instantiation
Function calls need to refer to the pre- and postcondition of the called function. In general, function definitions correspond to a universally quantified formula that are instantiated with the function call arguments.
function max(a, b) {
requires(typeof(a)=="number");
requires(typeof(b)=="number");
ensures(result => result >= a);
if (a > b) {
return a;
} else {
return b;
}
}
const x = max(23, 42);
assert(x >= 23);
In simple cases like this, the pre- and postconditions of a callee can be looked by function name. However, this is not generally possible, in particular for higher-order functions.
In the following example, the argument 23 needs to satisfy the precondition of f, i.e. $\texttt{pre} (f, 23)$ needs to be implied by the instantiated function definition of $f$.
In this example, the quantifier instantiation follows directly from the matching call. However, quantifier instantiations in SMT solvers are usually unrestricted and follow heuristics.
The following example uses the same code to show the verification condition before and after quantifier instantiation.
Higher-order Functions
For higher-order functions, a custom spec syntax can be used to specify a maximum pre- and a minimum postcondition. In verification conditions, this syntax translates to a quantifier - similar to function definitions.
With spec, the pre- and postconditions can refer to the function argument and the return value. Additionally, spec can also be nested. Is it therefore comparable to a dependent function type.
Classes and Class Invariants
In addition to simple data types such as booleans, numbers, strings, immutable arrays and simple immutable objects/records, the verifier also enables user-defined classes.
Similarly to function definitions and function calls, the invariant definition corresponds to a quantified formula that gets instantiated when accessing properties of a class instance. The following example shows a minimal class definition with an invariant that gets instantiated by the $\texttt{access}$ trigger.
Larger Examples
While this verifier is still an early prototype, it supports verification of some non-trivial applications:
- A custom integer list class and a reverse function such that reversing an ascending list yields a descending list ↗.
- A verified implementation of MergeSort such that returned lists are sorted ↗.
- A custom list class that can be parameterized by an invariant (somewhat analogous to "generics") ↗.
- A theorem and proof written in JavaScript showing that any locally increasing integer-ranged function is globally increasing. ↗.
Besides pre- and postconditions, these examples also use explicit triggers and other code that is solely used for verification purposes.
Formal Development of Program Verification with $\lambda^S$
In order to formally describe the program verification approach and prove its properties, we developed a pure functional core language $\lambda^S$ with with annotated pre- and postconditions written as logical propositions.
The syntax of $\lambda^S$ is in A-normal form, so its evaluation rules use variable bindings instead of substitution to simplify the proofs. As an example, the following annotated JavaScript function could be expressed in $\lambda^S$ as follows:
function inc (x) {
requires(Number.isInteger(x));
ensures(result => Number.isInteger(y) && result > x);
return x + 1;
}
...The verification rules of $\lambda^S$ resemble typing rules with verification conditions $ \langle P~\Rightarrow~Q \rangle$ whose validity is checked with an axiomatized SMT solver. As an example, the following verification rule for applying an unary operator $\otimes$ assumes a precondition $P$.
\[ \frac{\begin{matrix} x~\in~FV(P) \hspace{2ex} y~\not \in~FV(P) \hspace{2ex} \left \langle P~\Rightarrow~pre(\otimes, x) \right \rangle \\ P~\wedge~y = \otimes x~\vdash~e~:~Q\end{matrix}}{P~\vdash~\text{let}~y~=~\otimes x~\text{in}~e :~\exists y.~y = \otimes x~\wedge~Q} \]
The complete formal development can be found in the thesis. Most importantly, the following two theorems can be shown about $\lambda^S$:
Verification is sound: verified programs can be evaluated without getting stuck.
The verification algorithm is decidable: the decision procedure terminates for all inputs.
The proofs are specified and checked with the Lean Theorem Prover. The source code of the definitions, lemmas and proof steps can be found here.
Comparison with Refinement Types $\lambda^T$
Additionally, is is useful to compare static verification with static typing, so we introduced $\lambda^T$, a functional language with refined base types and dependent function types:
\[ T \in \text{Types} ~::=~ \{~x: B~|~ R~\} ~|~ x:T \rightarrow T \hspace{2.5em} B ~::=~ \text{Bool}~|~ \text{Int} \]
$\lambda^T$ programs can be translated to $\lambda^S:$
- Refined base types translate to type guards with
typeof. The refinements $R$ are a subset of $\lambda^S$ propositions $P$ and do not require translation. - Dependent function types translate to function specifications with
spec.
Well-typed $\lambda^T$ programs translate to verifiable $\lambda^S$ programs.
This proof is more complex than the previous two and still unfinished, primarily because of the quantifier instantiation algorithm. However, empirical evidence from manually translating example programs supports this conjecture.
To summarize: Static program verification can also be applied to dynamically-typed JavaScript programs including higher-order functions. The underlying quantifier instantiation algorithm ensures that the verification process remains predictable and avoids timeouts. Using a formalism, it can be shown that this verification approach is sound and (apparently) at least as expressive as refinement type systems such as LiquidHaskell.
Integrated Development and Verification Environments
If program verification fails, the verification errors are often hard to understand and error messages may not be sufficient to help the programmer resolve these issues. However, executable counterexamples and interactive verification tools can provide better feedback and assist the programmer in determining whether a verification issue corresponds to a bug in the code or an insufficient annotation or invariant.
Automatic Test Generation with Counterexamples
For failed verification conditions, the SMT solver returns a counterexample, i.e. an assignment of free variables to values that serve as a witness for the error. The following example shows a counterexample with values for a and b. Based on these values and the original code, a unit test is automatically generated in order to demonstrate the verification issue with a concrete assertion violation.
Counterexamples may not always correspond to bugs in the code that cause errors. In the following example, the fac function is lacking a postcondition. Multiplication requires both operands to be numbers, including n and the return value of fac(n - 1). However, the verifier cannot automatically infer the type of the return value due to recursion.
The generated test from the SMT counterexample does not produce an error or assertion violation. This suggests that the computation is actually correct but the verifier annotations insufficient. Indeed, adding ensures(res => typeof res === 'number'); as postcondition lets the verification succeed.
Counterexample Popups
The SMT counterexamples and test generation is the basis for an integrated development and verification environment.
As a simple editor/IDE extension, it is possible to show counterexample values of free variables as popups or tooltips in the editor itself. The following demo shows such an editor integration with an incorrect max function and instruction on how to use it.
Instructions
- Click the verify button to verify all assertions in the code.
- The second postcondition does not hold due to a bug in the implementation.
- Click on the red box in front of line 7 to select the verification condition.
- The editor now shows counterexample values for the free variables
aandb.
Verification Inspector
Error messages, tooltips and counterexample popups enable a brief overview of the verification issue. In order to present a more detailed explanation, an interactive verification inspector can be used. This inspector lists assumptions (such as preconditions and invariants) and the asserted logical statement. Furthermore, additional assumptions and assertions can be entered and tested by the user. This feature can be useful for interactive exploration and experimentation without having to change the original source code. This is analogous to the way interactive step-by-step debuggers are preferable to printf debugging.
Instructions
- Click the verify button to verify all assertions in the code.
- Click on the yellow triangle in front of line 5 to select the verification condition.
- The panel on the right lists assumptions and assertions and the editor shows values for the counterexample as popup markers.
- It seems the postcondition does not hold if
bis not a number. Check this hypothesis by enteringtypeof b === 'number'next to 'Assume:' and confirm this with by pressing the enter/return key. - With this additional assumption, the postcondition can now be verified.
Integrated Test Debugger
Finally, the automatically generated test can also be help with understanding verification issues. Instead of presenting automatically generated test code the programmer directly, the environment enables the programmer to step through the original code while showing variables in scope, the current call stack and letting the user query the (static) verifier state and (dynamic) test execution state with watch expressions.
Instructions
- Click the verify button to verify all assertions in the code.
- Click on the first incorrect verification condition in line 6.
- The verification inspector in the panel on the right lists watch expressions, variables in scope and the call stack.
- In this case, the counterexample uses
0for bothaandb. - To query the return value, enter
resnext to 'Watch:'. - It seems the function returns
undefined. - To see the control flow, step through the code by clicking Restart and then clicking Step Into about eight times.
- It seems none of the two
ifstatements returned a value when stepping through the code with this counterexample.
User Study
The integrated verification and development environment was evaluated with a user study with 18 participants. The user study focussed on how the proposed features can be used for smaller programming and verification tasks. Test subjects had no prior experience with the environment itself but indicated to have at least basic knowledge of JavaScript and might have used other program verifiers before.
The user study was conducted entirely online. Participants were presented with a brief introduction of the environment, followed by a series of programming and verification tasks, and finally surveyed about their experience using the tool.
The survey results are summarized in the tables below.
| Response (%) | Verification Inspector | Counterexample Popups | Integrated Debugger |
|---|---|---|---|
| Used this feature in experiments | 39 | 50 | 28 |
| Unsuccessfully tried using it | 33 | 33 | 22 |
| Did not use it | 27 | 17 | 50 |
| The feature is helpful | 33 | 55 | 44 |
| It could be helpful with different UI | 50 | 39 | 44 |
| It is not useful for development | 6 | 6 | 6 |
| It impairs the development process | 11 | 0 | 6 |
As part of the user study, participants ranked their JavaScript proficiency on a scale from 1 (novice) to 5 (export) and indicated whether they had prior experience with program verification.
| Experience with | JavaScript | Verification | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | no | yes | |
| # Participants | 1 | 2 | 3 | 6 | 6 | 8 | 10 |
| # successfully used at least one feature | 1 | 2 | 3 | 5 | 4 | 6 | 9 |
| # see features as potentially helpful | 1 | 2 | 3 | 6 | 6 | 8 | 10 |
The usage and the perceived benefits vary for the three main features of the environment. While half of the participants made use of counterexample popups, the verification inspector was only used by 39 percent of participants, and the integrated debugger by 28 percent. When features were used, they are generally seen as helpful or at least potentially helpful.
The programming tasks in the experiment may have been too small or simple to require debugging but the results might also indicate that the debugger integration might benefit the most from user interface improvements.
Finally, it is noteworthy that all participants, including those without JavaScript expertise or prior verification experience, found at least one of the the features helpful.
To summarize: Understanding and debugging verification errors can be difficult but executable counterexamples and an integrated development and verification environment can assist programmers. The environment enables inspection of verification conditions including the option to interactively add or remove assumptions and assertions. Additionally, the environment provides shows counterexample values in the editor and supports step-by-step debugging for failed verification conditions based on automatically generated tests. A user study found that the proposed features are generally seen as helpful.
Related Work and Acknowledgements
The work on live programming is closely related and partly inspired by Elm, TouchDevelop (especially the It's Alive paper), the work by Jonathan Edwards (including Subtext), and Smalltalk environments such as Squeak and Lively Kernel/ lively.next. I also want to thank my former teammates at CDG/Y Combinator Research.
In terms of program verification, Dafny and LiquidHaskell are both strong closely related and much more mature than esverify. Additionally, the Lean Theorem Prover has been immensely helpful for the formal development.
Finally, I am very thankful to my PhD advisor, Cormac Flanagan, and the programming language group at UC Santa Cruz, including Sohum Banerjea and Thomas Schmitz.
The idea for this kind of interactive thesis comes from Tomas Petricek and his interactive page on Coeffects.